Answer:
La partícula tiene una aceleración de -24 cuando t = 4.
Step-by-step explanation:
Sea
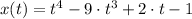 , donde
, donde
 y
y
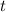 son la posición y el tiempo, respectivamente.
son la posición y el tiempo, respectivamente.
Físicamente, entendemos que la aceleración es la segunda derivada de la posición y la primera derivada de la velocidad. Entonces tenemos que la funciones de velocidad y posición son, respectivamente.
Velocidad
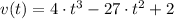
Aceleración
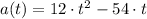
Si conocemos que
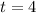 , entonces evaluamos la segunda derivada de la posición:
, entonces evaluamos la segunda derivada de la posición:
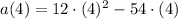
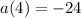
La partícula tiene una aceleración de -24 cuando t = 4.