Answer:
1) The engine torque is approximately 134.33 N·m
2) The speed of the engine is approximately 4,469.15 revolutions per minute
Explanation:
1) The drag coefficient,
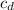 , is given by the formula;
, is given by the formula;
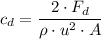
Where;
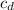 = 0.28
= 0.28
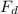 = The drag force
= The drag force
ρ = The fluid density = 0.00206 slugs/ft³ = 1.06168037 kg/m³
u = The object's flow speed = 130 mi/h = 58.1152 m/s
A = The frontal area = 19.8 ft² = 1.83948 m²
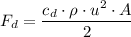
∴
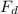 = (0.28 × 1.06168037 × (58.1152)² × 1.83948)/2 ≈ 923.4 N
= (0.28 × 1.06168037 × (58.1152)² × 1.83948)/2 ≈ 923.4 N
We have;

Where;
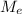 = The engine torque
= The engine torque
ε₀ = The overall gear reduction ratio = 2.5
 = The drivetrain efficiency = 0.88
= The drivetrain efficiency = 0.88
r = The wheel radius = 12.6 inches = 0.32004 meters

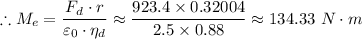
The engine torque =
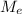 ≈ 134.33 N·m
≈ 134.33 N·m
The engine torque ≈ 134.33 N·m
2) The speed of the engine,
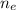 , is obtained from the following formula;
, is obtained from the following formula;
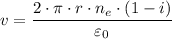
Where;
v = The vehicle's speed = 130 mi/h = 58.1152 m/s
r = The wheel radius = 12.6 inches = 0.32004 meters
i = The drive axle slippage = 3% = 3/100 = 0.03
ε₀ = The overall gear reduction ratio = 2.5
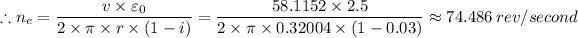
The speed of the engine in revolution per minute = 60 seconds/minute × 74.486 rev/second ≈ 4,469.15 revolutions per minute
The speed of the engine ≈ 4,469.15 revolutions per minute.