Answer:
The value of c is -1
g(x) = x² + 2x - 1, x ≥ -1
x must be greater than or equal -1 to make g(x) one-one function
Explanation:
- Any function that has an inverse must be a one-one function.
- In the quadratic function, we can not find its inverse because it is a many-one function
- If we restricted its domain at the x-coordinate of its vertex point it will be a one-one function so we can find its inverse
- If a point (x, y) lies on a function, then point (y, x) lies on its inverse
Let us use these notes to solve our question
∵ g(x) = x² + 2x +c, where x ≥ -1
∴ g(x) is quadratic function
∵ f(x) is the inverse of g(x)
∵ f(2) = 1
→ That means point (2, 1) lies on the graph of f(x)
∴ (2, 1) ∈ f(x)
→ Switch x and y to find the image of this point on g(x)
∴ (1, 2) lies on the graph of g(x)
∴ (1, 2) ∈ g(x)
→ T find c substitute x and g(x) by the coordinates of the point (1, 2)
∵ x = 1 and g(x) = 2
∴ 2 = (1)² + 2(1) + c
∴ 2 = 1 + 2 + c
∴ 2 = 3 + c
→ Subtract 3 from both sides to find c
∵ 2 - 3 = 3 - 3 + c
∴ -1 = c
∴ The value of c is -1
∴ g(x) = x² + 2x - 1
To find the x-coordinate of the vertex point of g(x) use this rule h =
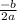 , where a is the coefficient of x² and b is the coefficient of x
, where a is the coefficient of x² and b is the coefficient of x
∵ a = 1 and b = 2
∴ h =
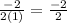
∴ h = -1
→ By using the 3rd note above we must restrict the domain at the
x-coordinate of its vertex
∵ The x-coordinate of g(x) is -1
∵ f(x) is the inverse of g(x)
∴ The domain of g(x) must be greater than or equal to -1
→ The domain is the values of x
∴ g(x) has an inverse if x ≥ -1
∴ x must be greater than or equal to -1 to make g(x) one-one function