Answer:
Your answers are below ↓
Explanation:
Given ↓
A) 2x-3y = 5 and 3x+4y = 6 ( The method this has to be solved in is the elimination method. )
Now using these,
(1)×3 - (2)×2 = 6x + 9y - 6x - 8y = 15 - 12
therefore,
y = 3
putting the value of y in eqn. (1)
2x + 6 = 5
therefore,
x = -1/2
B) y=x^2 - 2x and y = 2x -3 ( The method this has to be solved in is the substitution method. )
Reduce the greatest common factor on both sides of the equation:

Rearrange like terms to the same side of the equation:
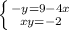
Divide both sides of the equation by the coefficient of the variable:
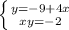
Substitute the unknown quantity into the elimination:
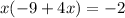
Apply Multiplication Distribution Law:

Reorder the equation:
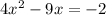
Divide the equation by the coefficient of the quadratic term:
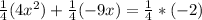
Calculate:
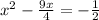
Add one term in order to complete the square:

Calculate:
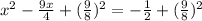
Factor the expression using
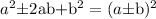 :
:
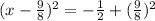
Simplify using exponent rule with the same exponent rule:
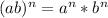

Calculate the power:
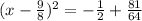
Find common denominator and write the numerators above the denominator:
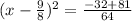
Calculate the first two terms:
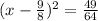
Rewrite as a system of equations:
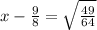 or
or
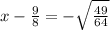
Rearrange unknown terms to the left side of the equation:
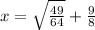
Rewrite the expression using
![\sqrt[n]{ab} =\sqrt[n]{a} *\sqrt[n]{b}](https://img.qammunity.org/2023/formulas/mathematics/college/rkc3ep654vwx6md6r12qga7ztwnc52vu6h.png) :
:
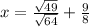
Factor and rewrite the radicand in exponential form:
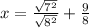
Simplify the radical expression:
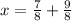
Write the numerators over the common denominator:
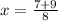
Calculate the first two terms:
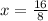
Reduce fraction to the lowest term by canceling the greatest common factor:

Rearrange unknown terms to the left side of the equation:
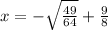
Rewrite the expression using
![\sqrt[n]{a} =\sqrt[n]{a} *\sqrt[n]{b}](https://img.qammunity.org/2023/formulas/mathematics/college/d0j3cgx2hlpux6bee028cu2uk8flwt82ar.png) :
:
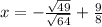
Factor and rewrite the radicand in exponential form:
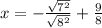
Simplify the radical expression:
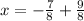
Write the numerators over common denominator:
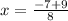
Calculate the first two terms:

Reduce fraction to the lowest term by canceling the greatest common factor:
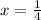
Find the union of solutions:
 or
or
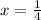
Substitute the unknown quantity into the elimination:
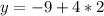
Calculate the first two terms:
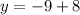
Calculate the first two terms:
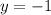
Substitute the unknown quantity into the elimination:

Reduce the expression to the lowest term:
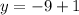
Calculate the first two terms:
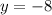
Write the solution set of equations:
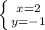 or
or
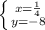 -------> Answer
-------> Answer
C) y=x^2 - 2x and y = 2x -3 ( This method this has to be solved in is the substitution method. )
Step 1: We start off by Isolating y in y = 2x - 3
y=2x-3 ----------> ( Simplify )
y+(-y)=2x-3+(-y) ---- > ( Add (-y)on both sides)
0=-3+2x-y
y/1 = 2x-3/1 --------> (Divide through by 1)
y = 2x - 3
We substitute the resulting values of y = 2x - 3 and y = x^2 - 2x
(2 * x - 3) = x^2 - 2x ⇒ 2x -3 = x^2 - 2x ----> ↓
(Substituting 2x - 3 for y in y = x^2 -2x )
Next: Solve (2x - 3 = x^2 - 2x) for x using the quadratic formular method
2x - 3 = x^2 - 2x
x = -b±b^2-4ac/2a Step 1: We use the quadratic formula with ↓
a = -1,b=4,c= - 3
x = -4±(4)^2-4(-1)(-3)/2(-1) Step 2: Substitute the values into the Quadratic Formular
x = -4± 4/ - 2 x = 1 or x = 3 Step 3: Simplify the Expression & Separate Roots
x = 1 or x = 3 ------- ANSWER
Substitute 1 in for x in y = 2x - 3 then solve for y
y = 2x - 3
y = 2 · (1) - 3 (Substituting)
y = -1 (Simplify)
Substitute 3 for in y = 2x - 3 then solve for y
y = 2x - 3
y = 2 · (3) - 3 (Substituting)
y = 3 (Simplify)
Therefore, the final solutions for y = x^2 -2x; y = 2x - 3 are
x₁ = 1, y₁ = -1
x₂ = 3, y₂ = 3