Consider,
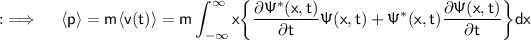
Multiply both sides by ih and simplification will yield
![{:\implies \quad \displaystyle \sf ih\langle p\rangle =m\int_(-\infty)^(\infty)x\bigg[\Psi (x,t)\bigg\{(h^2)/(2m)(\partial^(2)\Psi^(*)(x,t))/(\partial x^2)-V(x)\Psi^(*)(x,t)\bigg\}+\Psi^(*)(x,t)\bigg\{V(x)\Psi (x,t)-(h^2)/(2m)(\partial^(2)\Psi (x,t))/(\partial x^2)\bigg\}\bigg]dx}]()
Some simplification, Then Integrate by parts and then knowing the fact that the wave function vanishes for
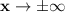 will yield:
will yield:
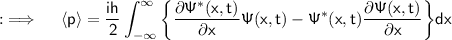
Integrating by parts and knowing the same fact by some simplification will yield:

The momentum is thus contained within the wave function, so we can then deduce that:
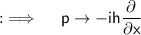
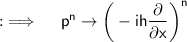
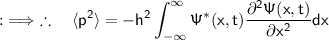
Now the kinetic energy
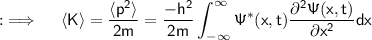
The classical formula for the total energy

Multiplying this equation by
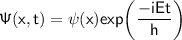 and use the above equations and simplify it we will be having
and use the above equations and simplify it we will be having
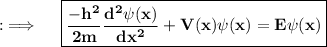
This is the Famous Time-Independent Schrödinger wave equation
Note:- If I write all the explanation then the Answer box willn't allow me to submit the answer