Question

The total surface area of cube is 864cmsquare. Find its volume.​

Answer 1

V = 1728 cm²

Explanation:

the faces of a cube are 6 congruent squares

given surface area = 864

then area of 1 face = 864 ÷ 6 = 144 cm²

now area of square = s² ( s is the side length ) , so

s² = 144 ( take square root of both sides )

s =
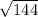`√(144)` = 12

the volume (V) of a cube is calculated as

V = s³ = 12³ = 1728 cm³