Answer:
V = 1728 cm²
Explanation:
the faces of a cube are 6 congruent squares
given surface area = 864
then area of 1 face = 864 ÷ 6 = 144 cm²
now area of square = s² ( s is the side length ) , so
s² = 144 ( take square root of both sides )
s =
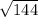 = 12
= 12
the volume (V) of a cube is calculated as
V = s³ = 12³ = 1728 cm³