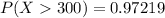Question

An Airliner has a capacity for 300 passengers. If the company overbook a flight with 320 passengers, What is the probability that it will not be enough seats to accommodate all passengers. Assume that the probability that a randomly selected passenger shows up to the airport is 0.96. Find the probability using the normal distribution as an approximation to the binomial distribution.

Answer 1

The probability is
`P(X  >300 ) = 0.97219`

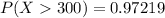
Explanation:

From the question we are told that

The capacity of an Airliner is k = 300 passengers

The sample size n = 320 passengers

The probability the a randomly selected passenger shows up on to the airport

`p = 0.96`

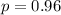
Generally the mean is mathematically represented as

`\mu  =  n*  p`

=>
`\mu  =  320 *  0.96`

=>
`\mu  = 307.2`

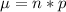
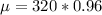
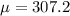
Generally the standard deviation is

`\sigma =  √(n *  p *  (1 -p ) )`

=>
`\sigma =  √(320  *  0.96 *  (1 -0.96 ) )`

=>
`\sigma =3.50`

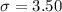
Applying Normal approximation of binomial distribution

Generally the probability that there will not be enough seats to accommodate all passengers is mathematically represented as

`P(X  > k ) =  P( ( X -\mu )/(\sigma )  >  (k - \mu)/(\sigma ) )`

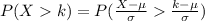
Here
`( X -\mu )/(\sigma )  =Z (The \ standardized \  value \  of  \ X )`

=>
`P(X  >300 ) =  P(Z >  (300 - 307.2)/(3.50) )`

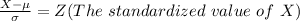
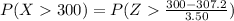
Now applying continuity correction we have

`P(X  >300 ) =  P(Z >  ([300+0.5] - 307.2)/(3.50) )`

=>
`P(X  >300 ) =  P(Z >  ([300.5] - 307.2)/(3.50) )`

=>
`P(X  >300 ) =  P(Z >  -1.914 )`

From the z-table

`P(Z >  -1.914 ) =  0.97219`

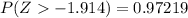
So

`P(X  >300 ) = 0.97219`