Question

A single-turn circular loop of radius 9.4 cm is to produce a field at its center that will just cancel the earth's field of magnitude 0.7 G directed at 70degrees below the horizontal north direction. Find the current in the loop.

Answer 1

The current in the loop is 10.5 A.

Step-by-step explanation:

Given that,

Radius = 9.4 cm

Magnetic field = 0.7 G

Angle = 70°

We know that,

The magnetic field due to the current in a loop is

`B_(I)=(\mu_(0)NI)/(2r)`

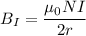
The magnetic field due to the current is equal to the magnetic field of earth.

`B_(E)=B_(I)=(\mu_(0)NI)/(2r)`

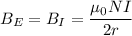
We need to calculate the current in the loop

Using formula of magnetic field

`B=(\mu_(0)NI)/(2r)`

`I=(2rB)/(\mu_(0)N)`

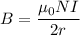
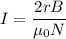
Put the value into the formula

`I=(2*9.4*10^(-2)*0.7*10^(-4))/(4\pi*10^(-7)*1)`

`I=10.5\ A`

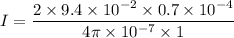
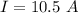
Hence, The current in the loop is 10.5 A.