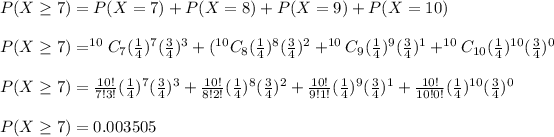Answer:
1)0.2502
2)0.475
3)0.003505
Explanation:
Total No. of question n= 10
There are four choices in each question
So, Probability of success
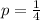
Probability of failure q =

We will use binomial over here
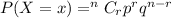
1)
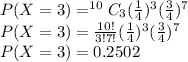
2)
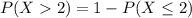
P(X>2)=1-(P(X=0)+P(X=1)+P(X=2))
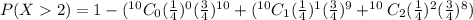

P(X>2)=0.475
3)