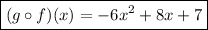Question

F(x) = 3x2 – 4x – 1
g(x) = –2x + 5
Find: (gof)(x)

Answer 1

`(g\circ f)(x)=-6x^2 +8x +7`

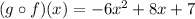
Explanation:

The Composite Function

Given f(x) and g(x) real functions, the composite function, named (g\circ f)(x) is defined as:

`(g\circ f)(x)=g(f(x))`

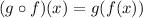
For practical purposes, it's found by substituting f into g.

Given the functions:

`f(x) = 3x^2 - 4x - 1`

`g(x) = -2x + 5`

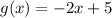
We need to find

`(g\circ f)(x)=g(f(x))`

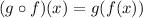
Replace f into g:

`(g\circ f)(x)=-2(3x^2 - 4x - 1) + 5`

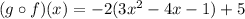
Operating:

`(g\circ f)(x)=-6x^2 +8x +2 + 5`

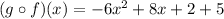
Reducing:

`(g\circ f)(x)=-6x^2 +8x +7`

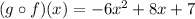
Thus,

`\boxed{(g\circ f)(x)=-6x^2 +8x +7}`