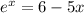Answer:
some part of your question is incomplete
attached below is the complete question
Answer :
F(0) = -5 < 0
F(1) = e - 1 > 0
since the functions : f(0) and f(1) have opposite signs then there is a 'c' whereby F(c) = 0 ( intermediate value theorem fulfilled )
Hence there is a root in the given equation :
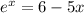
Step-by-step explanation:
using Intermediate value Theorem
If F(x) is continuous and f(a) and f(b) have opposite signs then there will be a'c'E (a,b) whereby F(c) = 0
given equation :
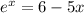 on (0,1)
on (0,1)
and F(x) =

This shows that the F(x) is continuous on (0,1)
F(0) =
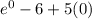 = -5 which is < 0
= -5 which is < 0
F(1) =
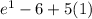 = e -1 > 0 and e = 2.7182
= e -1 > 0 and e = 2.7182
since the functions : f(0) and f(1) have opposite signs then there is a 'c' whereby F(c) = 0 ( intermediate value theorem fulfilled )
Hence there is a root in the given equation :