Given:
Total number of marbles = 15
Probability of randomly selecting a green marble =
 .
.
Probability of randomly selecting a green marble, replacing it, and then randomly selecting a blue marble =
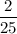 .
.
To find:
The number of blue marbles.
Solution:
Let the number of blue marbles be x.
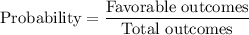
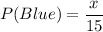
It is given that,
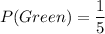
Probability of randomly selecting a green marble, replacing it, and then randomly selecting a blue marble is
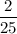 . So,
. So,
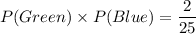
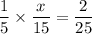
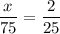
Multiply both sides by 75.
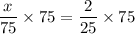
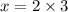
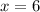
Therefore, the number of blue marbles in the bag is 6.