Question

A bag contains 15 marbles. The probability of randomly selecting a green marble is One-fifth. The probability of randomly selecting a green marble, replacing it, and then randomly selecting a blue marble is 2 over 25 . How many blue marbles are in the bag?

Answer 1

Given:

Total number of marbles = 15

Probability of randomly selecting a green marble =
`(1)/(5)`.

Probability of randomly selecting a green marble, replacing it, and then randomly selecting a blue marble =
`(2)/(25)`.

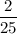To find:

The number of blue marbles.

Solution:

Let the number of blue marbles be x.

`\text{Probability}=\frac{\text{Favorable outcomes}}{\text{Total outcomes}}`

`P(Blue)=(x)/(15)`

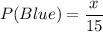
It is given that,

`P(Green)=(1)/(5)`

Probability of randomly selecting a green marble, replacing it, and then randomly selecting a blue marble is
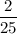`(2)/(25)`. So,

`P(Green)* P(Blue)=(2)/(25)`

`(1)/(5)* (x)/(15)=(2)/(25)`

`(x)/(75)=(2)/(25)`

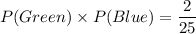
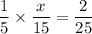
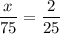
Multiply both sides by 75.

`(x)/(75)* 75=(2)/(25)* 75`

`x=2* 3`

`x=6`

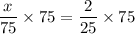
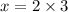
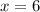
Therefore, the number of blue marbles in the bag is 6.