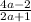Can you help me to solve this

Question

asked Dec 9, 2021 221k views

2 Answers

Haatschii · Answer 1 · 2021-12-14T22:20:19+0000

Answer:

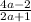
(4a-2)/(2a+1)

Explanation:

Factorise the numerator and denominator

8a² - 2 ← factor out 2 from each term

= 2(4a² - 1) ← 4a² - 1 is a difference of squares

= 2(2a - 1)(2a + 1)

4a² + 4a + 1 ← is a perfect square

= (2a + 1)²

Thus

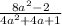
(8a^2-2)/(4a^2+4a+1)

=
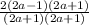(2(2a-1)(2a+1))/((2a+1)(2a+1)) ← cancel (2a + 1) on numerator/ denominator

=
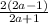
(2(2a-1))/(2a+1)

=
(4a-2)/(2a+1)