To solve for
 tangent will be used because, tan theta equals to opposite side length divide by adjacent side length. Therefore, option C is correct
tangent will be used because, tan theta equals to opposite side length divide by adjacent side length. Therefore, option C is correct
To solve for side
 in the right-angled triangle where
in the right-angled triangle where
 is the side opposite the
is the side opposite the
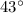 angle, and the adjacent side is 11 units, we use the tangent function. The tangent of an angle in a right triangle is the ratio of the length of the opposite side to the length of the adjacent side.
angle, and the adjacent side is 11 units, we use the tangent function. The tangent of an angle in a right triangle is the ratio of the length of the opposite side to the length of the adjacent side.
The formula for tangent is:
![\[\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}\]](https://img.qammunity.org/2021/formulas/mathematics/high-school/s0noarerfcqd60vv9j5bp6j7p2qh65q62m.png)
Substituting the given values into the formula:
![\[\tan(43^\circ) = (a)/(11)\]](https://img.qammunity.org/2021/formulas/mathematics/high-school/xjx4a8823ekeiz2kfmlcxegw1kh3ahrhlg.png)
To find
 , we rearrange the formula to solve for the opposite side:
, we rearrange the formula to solve for the opposite side:
![\[a = 11 * \tan(43^\circ)\]](https://img.qammunity.org/2021/formulas/mathematics/high-school/jtwg86ihsjem00fjkurs39k0rod92mp3f9.png)
Using a calculator, we find that
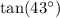 is approximately
is approximately
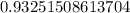 . Multiplying this by the length of the adjacent side (11 units), we get:
. Multiplying this by the length of the adjacent side (11 units), we get:
![\[a \approx 11 * 0.93251508613704 \approx 10.26 \text{ units}\]](https://img.qammunity.org/2021/formulas/mathematics/high-school/rguclnu13tldu266imh1rg41hv9lk46mfq.png)
Therefore, the length of side
 opposite the
opposite the
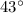 angle is approximately
angle is approximately
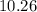 units.
units.