Question

How do you do this question?

Answer 1

Exact value:
`c = (-11+√(165))/(22)`

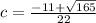
Approximate value: c = 0.08387

Round the approximate value however you need to

==============================================

Work Shown:

Let x = 1+c

`\displaystyle S = \sum_(n=2)^(\infty)(1+c)^(-n)\\\\\\\displaystyle S = \sum_(n=2)^(\infty)x^(-n)\\\\\\\displaystyle S = \sum_(n=2)^(\infty)(1)/(x^n)\\\\\\\displaystyle S = (1)/(x^2)+(1)/(x^3)+(1)/(x^4)\ldots\\\\\\`

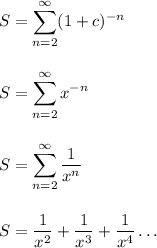
We have an infinite geometric series here. The first term is a = 1/(x^2). The common ratio is r = 1/x.

Each new term is found by multiplying the previous term by 1/x.

Assuming -1 < r < 1 is true, the infinite geometric sum is

`S = (a)/(1-r)\\\\\\S = (1/x^2)/(1-1/x)\\\\\\S = (1/x^2)/(x/x-1/x)\\\\\\S = (1/x^2)/((x-1)/x)\\\\\\S = (1)/(x^2)/(x-1)/(x)\\\\\\S = (1)/(x^2)*(x)/(x-1)\\\\\\S = (1)/(x^2-x)\\\\\\`

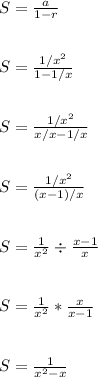
Plug in S = 11 and solve for x

`S = (1)/(x^2-x)\\\\11 = (1)/(x^2-x)\\\\11(x^2-x) = 1\\\\11x^2-11x = 1\\\\11x^2-11x-1 = 0\\\\`

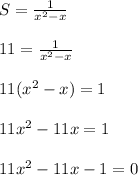
Use the quadratic formula to find the two solutions

`x = (11+√(165))/(22) \approx 1.08387\\\\x = (11-√(165))/(22) \approx -0.08387\\\\`

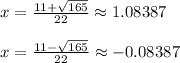
Using these x values, we find that the corresponding r values are

r = 1/x = 1/(1.08387) = 0.92262

r = 1/x = 1/(-0.08387) = -11.92321

The first r value makes -1 < r < 1 true, but the second r value does not. So we will be ignoring the solution x = -0.08387

----------------------------------------------

Using the solution that corresponds to x = 1.08387, we find the value of c is

`x = c+1\\\\c = x-1\\\\c = (11+√(165))/(22)-1\\\\c = (11+√(165))/(22)-(22)/(22)\\\\c = (11+√(165)-22)/(22)\\\\c = (-11+√(165))/(22)\\\\c \approx 0.08387\\\\`