Answer:
(a). The magnitude of the acceleration of the crate is 1.44 m/s².
(b). The direction of the crate is 34.60°.
Step-by-step explanation:
Given that,
Mass of crate = 26.1 kg
Coefficient of kinetic friction = 0.347
We need to calculate the resultant force
Using figure
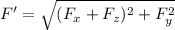
Put the value into the formula
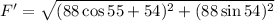
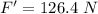
(a). We need to calculate the acceleration of the crate
Using formula of sum of force
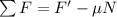
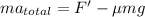
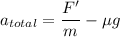
Put the value into thr formula
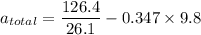
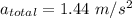
(b). We need to calculate the direction
Using formula of the direction
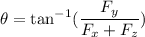
Put the value into the formula
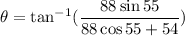

Hence, (a). The magnitude of the acceleration of the crate is 1.44 m/s².
The direction of the crate is 34.60°.