Question

An Alaskan rescue plane traveling 46 m/s drops a package of emergency rations from a height of 101 m to a stranded party of explorers. The acceleration of gravity is 9.8 m/s^2. Where does the package strike the ground relative to the point directly below where it was released? Answer in units of m.

Answer 1

The package strikes 207 m at the ground relative to the point.

Step-by-step explanation:

Given that,

Speed = 46 m/s

Height = 101 m

Acceleration = 9.8 m/s²

We need to calculate the time

Using equation of motion

`s=ut+(1)/(2)gt^2`

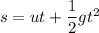
Put the value in the equation

`101=0+(1)/(2)*9.8* t^2`

`t=\sqrt{(2*101)/(9.8)}`

`t=4.5\ sec`

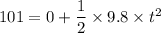
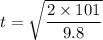
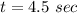
We need to calculate the distance where the package strikes

Using formula of distance

`x=vt`

Put the value into the formula

`x=46*4.5`

`x=207\ m`

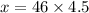
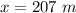
Hence, The package strikes 207 m at the ground relative to the point.