Answer:
114,126 (nearest whole number)
Explanation:
Geometric sequence
General form of a geometric sequence:

(where a is the first term and r is the common ratio)
Given:
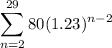
The sigma notation means to find the sum of the given geometric series where the first term is when n = 2 and the last term is when n = 29.
First term (a)
Determine the first term by substituting n = 2 into the given expression:
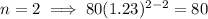
Common ratio (r)
From inspection, the common ratio is 1.23.
nth term
As the first term is when n = 2 and the last term is when n = 29, there is a total of 28 terms.
Therefore:
Sum of the first n terms of a geometric series:
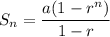
Substituting the given values into the formula:

Therefore, the sum of the given geometric series is 114,126 (nearest whole number)