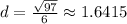2 Answers

NewNameStat · Answer 1 · 2021-12-22T08:07:06+0000

Answer:

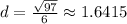
$d=(√(97))/(6)\approx1.6415$

Explanation:

We have the two points: (2, 5/2) and (8/3, 1).

And we want to find the distance between them.

So, we can use the distance formula:

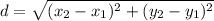
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2$

Let (2, 5/2) be (x₁, y₁) and let (8/3, 1) be (x₂, y₂). Substitute:

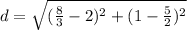
$d=\sqrt{((8)/(3)-2)^2+({1-(5)/(2))^2$

Evaluate the expressions within the parentheses. For the first term, we can change 2 to 6/3. For the second term, we can change 1 to 2/2. So:

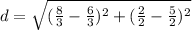
$d=\sqrt{((8)/(3)-(6)/(3))^2+({(2)/(2)-(5)/(2))^2$

Evaluate:

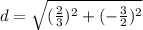
$d=\sqrt{((2)/(3))^2+(-(3)/(2))^2$

Square:

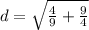
$d=\sqrt{(4)/(9)+(9)/(4)$

Add. We can change 4/9 to 16/36. And we can change 9/4 to 81/36. So:

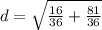
$d=\sqrt{(16)/(36)+(81)/(36)}$

Add:

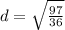
$d=\sqrt{(97)/(36)}$

We can separate the square roots:

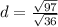
d=(√(97))/(√(36))

Simplify. So, our distance is:

$d=(√(97))/(6)\approx1.6415$

Please log in or register to add a comment.