Answer:
One base is
 inches for one of the bases and
inches for one of the bases and
 inches for the other base.
inches for the other base.
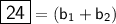 . Use guess and check to find two numbers that add to
. Use guess and check to find two numbers that add to
 with one number 6 more than the other to get
with one number 6 more than the other to get
 inches for one of the bases and
inches for one of the bases and
 inches for the other base.
inches for the other base.
Explanation:
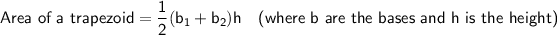
Given:
Substitute given values into the formula to find (b₁ + b₂) :
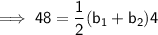
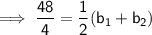
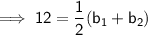

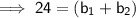
Therefore:
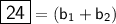
Let:
- Base b₁ = x in
- Base b₂ = (x + 6) in
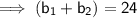
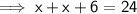
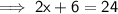
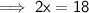

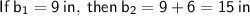
Therefore,
- Base b₁ = 9 in
- Base b₂ = 15 in