Question

The distribution of IQ scores for students at a large university are known to be approximately normally distributed with σ = 15. One student claims that the mean IQ for all students at the university is 100. A. Assuming that the student’s claim is true (that µ = 100), what is the probability of obtaining a simple random sample of 20 students whose mean IQ score is greater than 108. B. Suppose that you actually did collect a simple random sample of 20 students and found their mean IQ score was greater than 108. Would this give you good evidence to suggest that the mean IQ for all students at the school is greater than 100? Explain.

Answer 1

A

The probability of obtaining a simple random sample of 20 students whose mean IQ score is greater than 108 is

`P(\= X > 108) = 0.0084242`

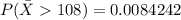
B

Comparing the p-value obtained with a low level of significance (say ∝= 0.01 ) we see that the p-value is less than ∝ which implies that the null hypothesis is rejected hence we can state that there is sufficient evidence to conclude that the mean IQ for all students at the school is greater than 100

Explanation:

From the question we are told that

The standard deviation is
`\sigma = 15`

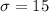
The population mean is
`\mu = 100`

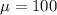
The sample size n = 20

Generally the standard deviation of the sample mean (standard error ) is mathematically represented as

`\sigma_(\= x) = (\sigma )/(√(n) )`

=>
`\sigma_(\= x) = (15 )/(√(20) )`

=>
`\sigma_(\= x) = 3.35`

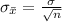
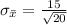
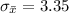
Generally the probability of obtaining a simple random sample of 20 students whose mean IQ score is greater than 108 is mathematically represented as

`P(\= X > 108) = P((\=X - \mu)/(\sigma_(\= x) ) > (108 - 100)/(3.35) )`

=>
`P(\= X > 108) = P(Z > (108 - 100)/(3.35) )`

=>
`P(\= X > 108) = P(Z > (108 - 100)/(3.35) )`

=>
`P(\= X > 108) = P(Z >2.39 )`

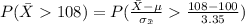
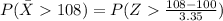
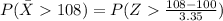
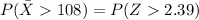
From the z-table

`P(z > 2.39) = 0.0084242`

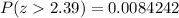
So

`P(\= X > 108) = 0.0084242`

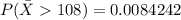
The null hypothesis is
`H_o : \mu = 100`

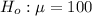
The alternative hypothesis is
`H_a : \mu > 100`

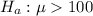
The sample mean is
`\= x = 108`

Generally the test statistics is = 2.39

Generally the p-value is equal to 0.0084242

Now comparing the p-value with a low level of significance (say ∝= 0.01 ) we see that the p-value is less than ∝ which implies that the null hypothesis is rejected and we can conclude that there is sufficient evidence to conclude that the mean IQ for all students at the school is greater than 100