Answer:
A
The probability of obtaining a simple random sample of 20 students whose mean IQ score is greater than 108 is
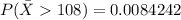
B
Comparing the p-value obtained with a low level of significance (say ∝= 0.01 ) we see that the p-value is less than ∝ which implies that the null hypothesis is rejected hence we can state that there is sufficient evidence to conclude that the mean IQ for all students at the school is greater than 100
Explanation:
From the question we are told that
The standard deviation is
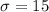
The population mean is
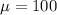
The sample size n = 20
Generally the standard deviation of the sample mean (standard error ) is mathematically represented as
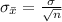
=>
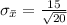
=>
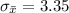
Generally the probability of obtaining a simple random sample of 20 students whose mean IQ score is greater than 108 is mathematically represented as
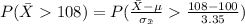
=>
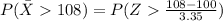
=>
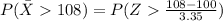
=>
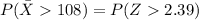
From the z-table
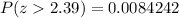
So
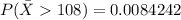
The null hypothesis is
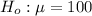
The alternative hypothesis is
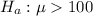
The sample mean is
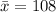
Generally the test statistics is = 2.39
Generally the p-value is equal to 0.0084242
Now comparing the p-value with a low level of significance (say ∝= 0.01 ) we see that the p-value is less than ∝ which implies that the null hypothesis is rejected and we can conclude that there is sufficient evidence to conclude that the mean IQ for all students at the school is greater than 100