Question

Lee is a teacher at a local high school who wanted to assess whether or not dogs physically resemble their owners enough for people to be able to correctly match a dog to their owner better than if just guessing. Lee, who is also a dog owner, showed pictures of two dogs to her class of 16 students. One photo was of the teacher's dog (Yoda) and the other photo was of a dog the teacher had never met. The students were asked to guess which dog was actually the teacher's. If dogs do not physically resemble their owners, the students would get a correct match with probability 0.50. It turned out that 14 of the 16 students correctly picked out the teacher's dog. Does it appear that the population proportion of people who can correctly match a dog to their owner (out of two options) is better than just guessing? The hypotheses to be tested are H0: p = 0.50 versus Ha: p > 0.50, where the parameter p represents the population proportion of all people who can correctly match a dog to their owner (out of two options).

Answer 1

Explanation:

Given that:

The null hypothesis:

`H_0: p = 0.50`

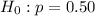
The alternative hypothesis:

`H_a : p> 0.50`

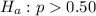
Suppose the number of samples n from the population is 16

The observed value x of the test statistics for testing the hypothesis for this study is x = 14

However, if the null hypothesis is true, then the distribution of the test statistics follows a binomial distribution which is expressed as:

bin(n=16, p = 0.5) distribution

The p-value for this test statistics can be computed as:

p-value = P(X ≥ 14)

p-value = 1 - P (X ≤ 13)

p-value =
`1- \sum _(x=0^(x-1)) (n^C \ _x)p^x(q)^((n-x))`

p-value =
`1- \sum _(x=0^(x-1)) (n!)/(r!(n-r)! ) p^x(q)^((n-x))`

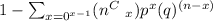
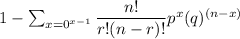
p-value = 0.00209