Answer:
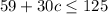
2 rooms
Explanation:
Given
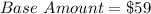
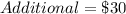 per carpet
per carpet

Required
Write an inequality to determine the situation
Represent the number of carpets with c
First, we need to determine an expression for the cleaner's charges:
This is:
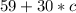
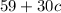
Since the customer's budget do not exceed $125.
This implies that the cleaner's charges must be less than or equal to the budget.
So, we have:
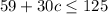
Solving further: [Collect Like Terms]
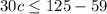

Divide through by 30
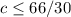
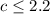
Since number of rooms can't be fraction;
The maximum number of rooms the customer can afford is 2