Answer:
f(x) is increasing for all x > –4
Explanation:
Given function:
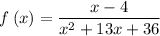
Asymptote: a line which the curve gets infinitely close to, but never touches.
As the degree of the denominator is larger than the degree of the numerator, there is a horizontal asymptote at y = 0 for the left part of the curve.
To find the vertical asymptotes, set the denominator to zero and solve for x.
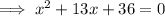

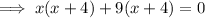
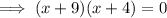


Therefore, the vertical asymptotes are:
Input x-values either side of the vertical asymptotes into the function:
when x < -9
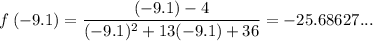
when x > -4
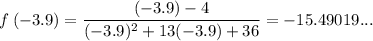
A function is said to be increasing if the y-values increase as the x-values increase.
A function is said to be decreasing if the y-values decrease as the x-values increase.
Since we know that as x < -9 the function approaches zero, and at x = -9.1 the function is -25.7, then the function is decreasing for the domain (-∞, -9).
As the function is zero when x = 4, and f(-3.9)=-15.5, we can conclude that the function is increasing for the domain (-4, ∞)
Therefore, the only true statement is:
f(x) is increasing for all x > –4