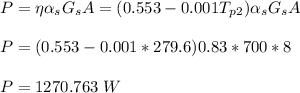Question

A photovoltaic panel of dimension 2 m × 4 m is installed on the roof of a home. The panel is irradiated with a solar flux of GS = 700 W/m2 , oriented normal to the top panel surface. The absorptivity of the panel to the solar irradiation is αS = 0.83, and the efficiency of conversion of the absorbed flux to electrical power is η = P/αSGSA = 0.553 − 0.001 K−1 Tp, where Tp is the panel temperature expressed in kelvins and A is the solar panel area. Determine the electrical power generated for (a) a still summer day, in which Tsur = T[infinity] = 35°C, h = 10 W/m2 ⋅K, and (b) a breezy winter day, for which Tsur = T[infinity] = −15°C, h = 30 W/m2 ⋅K. The panel emissivity is ε = 0.90

Answer 1

(a) the electrical power generated for still summer day is 1013.032 W

(b)the electrical power generated for a breezy winter day is 1270.763 W

Step-by-step explanation:

Given;

Area of panel = 2 m × 4 m, = 8m²

solar flux GS = 700 W/m²

absorptivity of the panel, αS = 0.83

efficiency of conversion, η = P/αSGSA = 0.553 − 0.001 K⁻¹ Tp

panel emissivity , ε = 0.90

Apply energy balance equation to determine he electrical power generated;

transferred energy + generated energy = 0

(radiation + convection) + generated energy = 0

`[\alpha_sG_s-\epsilon \alpha(T_p^4-T_s^4)]-h(T_p-T_\infty) - \eta \alpha_s G_s = 0`

`[\alpha_sG_s-\epsilon \alpha(T_p^4-T_s^4)]-h(T_p-T_\infty) - (0.553-0.001T_p)\alpha_s G_s`

(a) the electrical power generated for still summer day

`T_s = T_(\infty) = 35 ^oC = 308 \ k`

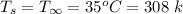
`[0.83*700-0.9*5.67*10^(-8)(T_p_1^4-308^4)]-10(T_p_1-308) - (0.553-0.001T_p_1)0.83*700 = 0\\\\3798.94-5.103*10^(-8)T_p_1^4 - 9.419T_p_1 = 0\\\\Apply \ \ iteration \ method \ to \ solve \ for \ T_p_1\\\\T_p_1 = 335.05 \ k`

`P = \eta \alpha_s G_s A = (0.553-0.001 T_p_1)\alpha_s G_s A \\\\P = (0.553-0.001 *335.05)0.83*700*8 \\\\P = 1013.032 \ W`

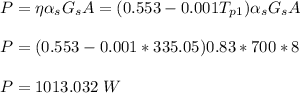
(b)the electrical power generated for a breezy winter day

`T_s = T_(\infty) = -15 ^oC = 258 \ k`

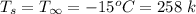
`[0.83*700-0.9*5.67*10^(-8)(T_p_2^4-258^4)]-10(T_p_2-258) - (0.553-0.001T_p_2)0.83*700 = 0\\\\8225.81-5.103*10^(-8)T_p_2^4 - 29.419T_p_2 = 0\\\\Apply \ \ iteration \ method \ to \ solve \ for \ T_p_2\\\\T_p_2 = 279.6 \ k`

`P = \eta \alpha_s G_s A = (0.553-0.001 T_p_2)\alpha_s G_s A \\\\P = (0.553-0.001 *279.6)0.83*700*8 \\\\P = 1270.763 \ W`