Problem 1
Answer: C) No solution
---------------------------
Step-by-step explanation:
We have z = -4 and 4z = -4 at the same time. Solving 4z = -4 leads to z = -1
So in effect we have z = -4 and z = -1 at the same time, but this is a contradiction. A variable can only hold one number at a time.
======================================================
Problem 2
Answer: C) Infinitely many solutions
---------------------------
Step-by-step explanation:
The two equations are equivalent. You can prove as such by isolating 2y in the first equation.
5x = 8-2y
5x+2y = 8
2y = 8-5x
2y = -5x+8
-5x+8 = 2y
This shows the first equation is equivalent to the second, and vice versa. They both graph the same line. Any point along the line is a solution. So that's why there are infinitely many of them.
======================================================
Problem 3
Answer: Choice A)
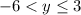
---------------------------
Step-by-step explanation:
The range is the set of the possible y values. We're concerned with every y coordinate of each (x,y) solution. So we only focus on the shaded region.
The dashed line means we exclude the boundary. It's an electric fence we cannot touch. So y > -6 or -6 < y describes part of the range
The other part is
 since y = 3 is the when the highest point occurs.
since y = 3 is the when the highest point occurs.
So writing
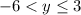 describes all possible y values of each (x,y) solution in the shaded region.
describes all possible y values of each (x,y) solution in the shaded region.