Question

Please help me, thank you

Answer 1

Problem 1

Answer: C) No solution

---------------------------

Step-by-step explanation:

We have z = -4 and 4z = -4 at the same time. Solving 4z = -4 leads to z = -1

So in effect we have z = -4 and z = -1 at the same time, but this is a contradiction. A variable can only hold one number at a time.

======================================================

Problem 2

Answer: C) Infinitely many solutions

---------------------------

Step-by-step explanation:

The two equations are equivalent. You can prove as such by isolating 2y in the first equation.

5x = 8-2y

5x+2y = 8

2y = 8-5x

2y = -5x+8

-5x+8 = 2y

This shows the first equation is equivalent to the second, and vice versa. They both graph the same line. Any point along the line is a solution. So that's why there are infinitely many of them.

======================================================

Problem 3

Answer: Choice A)
`-6 < y \le 3`

---------------------------

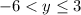
Step-by-step explanation:

The range is the set of the possible y values. We're concerned with every y coordinate of each (x,y) solution. So we only focus on the shaded region.

The dashed line means we exclude the boundary. It's an electric fence we cannot touch. So y > -6 or -6 < y describes part of the range

The other part is
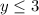`y \le 3` since y = 3 is the when the highest point occurs.

So writing
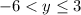`-6 < y \le 3` describes all possible y values of each (x,y) solution in the shaded region.