Answer:
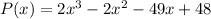
Step-by-step explanation:
Let the original polynomial be
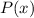 .
.
We know that when it is divided by
 , the quotient is
, the quotient is
 and we get a remainder of 3.
and we get a remainder of 3.
Therefore, this means that:
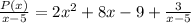
Remember what it means when we have a remainder. Say we have 13 divided by 3. Our quotient will be 4 R1, or 4 1 over 3. We put the remainder over the divisor. This is the same thing for polynomials.
So, to find our original polynomial, multiply both sides by
 :
:
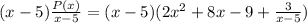
The left side will cancel. Distribute the right:

Distribute:

Combine like terms:
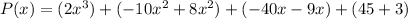
Evaluate:
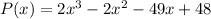
And we're done!