Question

Seven little spheres of mercury, each with a diameter of 2 mm. When they coalesce to form a single sphere, how big will it be (i.e. what is its diameter)? How does its surface area compare with the total surface area of the previous Seven little spheres?

Answer 1

The total surface area of the seven little spheres is 1.91 times the total surface area of the bigger sphere.

Step-by-step explanation:

Volume of a Sphere

The volume of a sphere of radius r is given by:

`\displaystyle V=(4)/(3)\cdot \pi\cdot r^3`

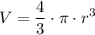
The volume of each little sphere is:

`\displaystyle V_l=(4)/(3)\cdot \pi\cdot 2^3`

`V_l=33.51\ mm^3`

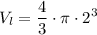
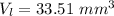
When the seven little spheres coalesce, they form a single bigger sphere of volume:

`V_b=7*V_l=234.57\ mm^3`

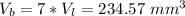
Knowing the volume, we can find the radius rb by solving the formula for r:

`\displaystyle V_b=(4)/(3)\cdot \pi\cdot r_b^3`

Multiplying by 3:

`3V_b=4\cdot \pi\cdot r_b^3`

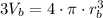
Dividing by 4π:

`\displaystyle (3V_b)/(4\cdot \pi)= r_b^3`

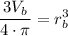
Taking the cubic root:

`\displaystyle r_b=\sqrt[3]{(3V_b)/(4\cdot \pi)}`

Substituting:

`\displaystyle r_b=\sqrt[3]{(3*234.57)/(4\cdot \pi)}`

`r_b=3.83\ mm`

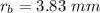
The surface area of the seven little spheres is:

`A_l=7*(4\pi r^2)=7*(4\pi 2^2)=351.86\ mm^2`

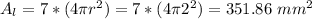
The surface area of the bigger sphere is:

`A_b=4\pi r_b^2=4\pi (3.83)^2=184.33\ mm^2`

The ratio between them is:

`\displaystyle (351.86\ mm^2)/(184.33\ mm^2)=1.91`

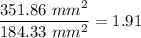
The total surface area of the seven little spheres is 1.91 times the total surface area of the bigger sphere.