Answer:
The total surface area of the seven little spheres is 1.91 times the total surface area of the bigger sphere.
Step-by-step explanation:
Volume of a Sphere
The volume of a sphere of radius r is given by:
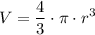
The volume of each little sphere is:
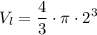
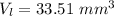
When the seven little spheres coalesce, they form a single bigger sphere of volume:
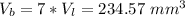
Knowing the volume, we can find the radius rb by solving the formula for r:
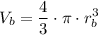
Multiplying by 3:
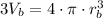
Dividing by 4π:
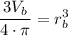
Taking the cubic root:
![\displaystyle r_b=\sqrt[3]{(3V_b)/(4\cdot \pi)}](https://img.qammunity.org/2021/formulas/physics/college/syvce5hqylp5ygvvlge2e0dzaj3qavoyex.png)
Substituting:
![\displaystyle r_b=\sqrt[3]{(3*234.57)/(4\cdot \pi)}](https://img.qammunity.org/2021/formulas/physics/college/u5a0fae7jmvgwbt2nrsdfabyoh09juv1zu.png)
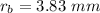
The surface area of the seven little spheres is:
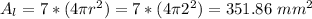
The surface area of the bigger sphere is:
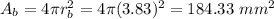
The ratio between them is:
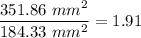
The total surface area of the seven little spheres is 1.91 times the total surface area of the bigger sphere.