Answer:
The measures of the two angles are 12° and 78°
Explanation:
Let us explain what is the complementary angles
Two angles are complementary if the sum of their measures is 90°
Example:
If m∠x + m∠y = 90°, then
∠x and ∠y are complementary angles
Let us solve the question
Assume that the measure of one of the complementary angle is x°
∵ The measure of its complementary is 66° more than it
∴ The measure of its complementary = x + 66
∵ The sum of the measures of the complementary angles is 90°
∴ x + 66 + x = 90
→ Add the like terms in the left side
∴ 2x + 66 = 90
→ Subtract 66 from both sides
∴ 2x + 66 - 66 = 90 - 66
∴ 2x = 24
→ Divide both sides by 2
∴
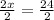
∴ x = 12°
→ Substitute the value of x in the second angle to find x
∵ The measure of the other angle = 12 + 66
∴ The measure of the other angle = 78°
∴ The measures of the two angles are 12° and 78°