Question

Consider a convergent duct with an inlet area A1 = 5 m2. Air enters this duct with a velocity V1=10m/s and leaves the duct exit with a velocity V2=30 m/s.

Required:
a. What is the area of the duct exit?
b. If the air pressure and temperature at the inlet area are 1.2 x105 N/m2, and 300K, respectively, what is the pressure at the exit?

Answer 1

(a) The area of the duct exit is 1.67 m²

(b) The air pressure at the exit is 1.195 x 10⁵ N/m²

Step-by-step explanation:

Given;

inlet area, A₁ = 5 m²

inlet velocity, V₁ = 10 m/s

exit velocity, V₂ = 30 m/s

(a) The area of the duct exit is determined by applying continuity equation;

A₁V₁ = A₂V₂

Where;

A₂ is the area of the duct exit

A₂ = (A₁V₁) / (V₂)

A₂ = (5 x 10) / (30)

A₂ = 1.67 m²

(b) Apply Bernoulli’s equation to determine the pressure at the exit;

`P_1 + (\rho V_1^2)/(2) = P_2 + (\rho V_2^2)/(2)\\\\P_2 = P_1 + (\rho V_1^2)/(2) - (\rho V_2^2)/(2)\\\\P_2 = P_1 + (\rho )/(2) (V_1^2 - V_2^2)`

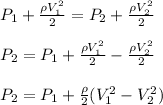
Density of air at 300k = 1.177 kg/m³

`P_2 = P_1 + (\rho )/(2) (V_1^2 - V_2^2)\\\\P_2 = 1.2*10^5 \ + \ (1.177)/(2) (10^2 - 30^2)\\\\P_2 = 1.2*10^5 \ + \ -470.8\\\\P_2 = 1.195*10^5 \ N/m^2`

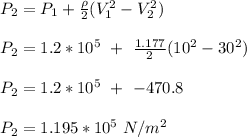
Therefore, the air pressure at the exit is 1.195 x 10⁵ N/m²