Question

The linear function y=2x+28 models the average cost of a haircut in a certain city, where y, is the average price of a haircut x years after 2000. Find the slope for the model. Then describe what this means in terms of the unit rate of change in the average cost of a haircut over time.

Answer 1

The slope of the model is
`m = 2\,(USD)/(yr)`.

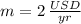The value of the slope indicates that the average cost of a hair cut is increased by 2 US dollars each year.

Explanation:

We have to notice that given function is a linear function, that is, a first order polynomial, whose standard form is described below:

`y =m\cdot x + b`

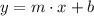
Where:

`m` - Slope, dimensionless.

`x` - Independent variable, dimensionless.

`y` - Dependent variable, dimensionless.

`b` - y-Intercept, dimensionless.

In this case, we use the linear function
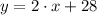`y = 2\cdot x + 28`, where
`x` is the time after 2000, measured in years, and
`y` is the average cost of a hair cut. The slope of the model is
`m = 2\,(USD)/(yr)`.

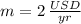The value of the slope indicates that the average cost of a hair cut is increased by 2 US dollars each year.