Answer:
The slope of the model is
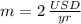 .
.
The value of the slope indicates that the average cost of a hair cut is increased by 2 US dollars each year.
Explanation:
We have to notice that given function is a linear function, that is, a first order polynomial, whose standard form is described below:
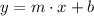
Where:
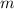 - Slope, dimensionless.
- Slope, dimensionless.
 - Independent variable, dimensionless.
- Independent variable, dimensionless.
 - Dependent variable, dimensionless.
- Dependent variable, dimensionless.
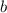 - y-Intercept, dimensionless.
- y-Intercept, dimensionless.
In this case, we use the linear function
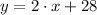 , where
, where
 is the time after 2000, measured in years, and
is the time after 2000, measured in years, and
 is the average cost of a hair cut. The slope of the model is
is the average cost of a hair cut. The slope of the model is
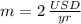 .
.
The value of the slope indicates that the average cost of a hair cut is increased by 2 US dollars each year.