A 0.50-kg ball, attached to the end of a horizontal cord, is rotated in a circle of radius 1.9 m on a frictionless horizontal surface. If the cord will break when the tension in…

Question

asked Nov 20, 2023 227k views

1 Answer

Professor Falken · Answer 1 · 2023-11-26T22:52:22+0000

Answer:

$\boxed {\boxed {\sf 18 \ m/s}}$

Step-by-step explanation:

The ball is moving in a circle, so the force is centripetal.

One formula for calculating centripetal force is:

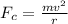
$F_c= \frac{mv^2}r}$

The mass of the ball is 0.5 kilograms. The radius is 1.9 meters. The centripetal force is 85 Newtons or 85 kg*m/s².

Substitute the values into the formula.

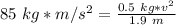
$85 \ kg*m/s^2 = (0.5 \ kg *v^2)/(1.9 \ m)$

Isolate the variable v. First, multiply both sides by 1.9 meters.

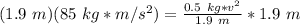
$(1.9 \ m)(85 \ kg*m/s^2) = (0.5 \ kg *v^2)/(1.9 \ m)*1.9 \ m$

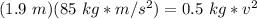
$(1.9 \ m)(85 \ kg*m/s^2) = {0.5 \ kg *v^2}$

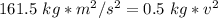
$161.5 \ kg*m^2/s^2 = 0.5 \ kg*v^2$

Divide both sides by 0.5 kilograms.

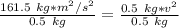
$\frac {161.5 \ kg*m^2/s^2}{0.5 \ kg} = (0.5 \ kg*v^2)/(0.5 \ kg)$

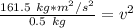
$\frac {161.5 \ kg*m^2/s^2}{0.5 \ kg} =v^2$

$323 \ m^2/s^2 = v^2$

Take the square root of both sides of the equation.

$\sqrt {323 \ m^2/s^2} =\sqrt{ v^2$

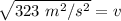
$\sqrt {323 \ m^2/s^2} =v$

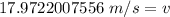
$17.9722007556 \ m/s =v$

The original measurements have 2 significant figures, so our answer must have the same.

For the number we found, 2 sig fig is the ones place. The 9 in the tenth place tells us to round the 7 to an 8.

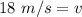
$18 \ m/s =v$

The maximum speed is approximately 18 meters per second.