Question

I need help on this, please explain how you get the result.

Answer 1

`x=5`

Explanation:

We have the equation:

`34\cdot 3^(x-2)-2\cdot 3^(x-3)=0.8\cdot 10^(x-2)+10^(x-3)`

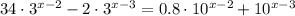
Let's simplify this a bit. Let
`u=x-2`. Then
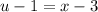`u-1=x-3`. We can substitute the exponents:

`34\cdot3^u-2\cdot 3^(u-1)=0.8\cdot 10^u+10^(u-1)`

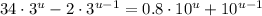
Use the properties of exponents, we can write
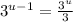`3^(u-1)=(3^u)/(3)`. We can do the same thing on the right. So:

`34\cdot3^u-2\cdot (3^u)/(3)=0.8\cdot 10^u+(10^u)/(10)`

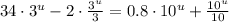
We can now factor out a
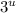`3^u` from the left and a
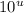`10^u` on the right. This yields:

`3^u(34-2\cdot(1)/(3))=10^u(0.8+ (1)/(10))`

Evaluate the expressions within the parentheses:

`3^u(34-(2)/(3))=10^u((9)/(10))`

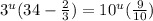
Evaluate:

`3^u((100)/(3))=10^u((9)/(10))`

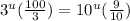
Now, let's multiply both sides by
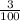`(3)/(100)`. So:

`3^u=10^u((9)/(10))((3)/(100))`

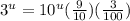
Also, let's divide both sides by
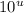`10^u`. Multiply on the right:

`(3^u)/(10^u)=(27)/(1000)`

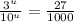
Therefore:

`3^u=27\text{ and } 10^u=1000`

We can now substitute back u. Notice that 27 is the same as 3 cubed and 1000 is the same as 10 cubed. So:

`3^(x-2)=3^3\text{ and } 10^(x-2)=10^3`

Since they have the same base, their exponents must be equal. Therefore:

`x-2=3`

Add 2 to both sides:

`x=5`

So, the value of x is 5.

And we're done!