Answer:
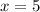
Explanation:
We have the equation:
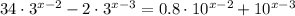
Let's simplify this a bit. Let
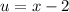 . Then
. Then
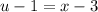 . We can substitute the exponents:
. We can substitute the exponents:
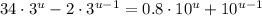
Use the properties of exponents, we can write
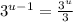 . We can do the same thing on the right. So:
. We can do the same thing on the right. So:
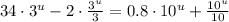
We can now factor out a
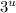 from the left and a
from the left and a
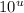 on the right. This yields:
on the right. This yields:
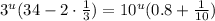
Evaluate the expressions within the parentheses:
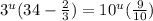
Evaluate:
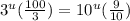
Now, let's multiply both sides by
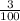 . So:
. So:
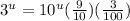
Also, let's divide both sides by
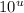 . Multiply on the right:
. Multiply on the right:
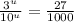
Therefore:
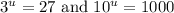
We can now substitute back u. Notice that 27 is the same as 3 cubed and 1000 is the same as 10 cubed. So:
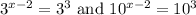
Since they have the same base, their exponents must be equal. Therefore:
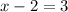
Add 2 to both sides:
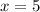
So, the value of x is 5.
And we're done!