Part (a)
This sequence is convergent because all we care about are the leading terms for the numerator and denominator. As n gets really large, the leading terms dictate what happens.
The leading term up top is 9n
The leading term down below is 7n
Divide the two items to get (9n)/(7n) = 9/7
We don't have to worry about dividing by zero because n will go off to infinity, and as it does so, the sequence
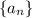converges to 9/7
========================================================
Part (b)
As n heads to infinity, the terms of the sequence are approaching 9/7 (they never quite hit the exact value though).
Note how 9/7 = 1.2857 approximately which is larger than 0
So effectively for very large values of n, we're adding on 1.2857 each time or close to it, meaning that this infinite series diverges.
------
For a series like this to converge, the answer to part (a) must be 0. This way at some point, we're effectively adding 0 to the series and we approach some fixed sum.
For example, consider the sequence 1/(7n+1)
As n goes to infinity, the terms of the sequence approach 0
This means that for some very large n, the 1/(7n+1) is basically 0 and we aren't adding much onto the sum to change it. So this sum will converge to a fixed value.