4 Answers: A, B, C, D
=======================================================
Step-by-step explanation:
f(x) is continuous when x >= 1. The only discontinuity for f(x) is when x = 0, but 0 is not part of this interval.
f(x) is positive for any valid x value in the domain since x^6 is always positive. In general, x^n is positive for all x when n is any even number.
f(x) is decreasing. You can see this through a table of values or through a graph. For anything in the form 1/(x^k), it will be a decreasing function because x^k gets larger, so 1/(x^k) gets smaller, when x goes to infinity.
--------------------
The conditions to use the integral test have been met. So we have to see if
 converges or not.
converges or not.
Let's integrate and find out

So we have
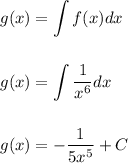
Meaning that,
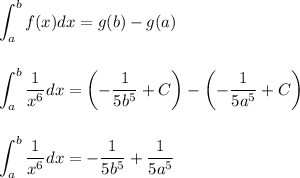
If we plug in a = 1 and apply the limit as b approaches positive infinity, then the expression
 will turn into
will turn into
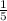
Therefore,
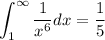
Because this integral converges, this means the series
 also converges as well by the integral test.
also converges as well by the integral test.