Answer:
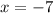
Explanation:
Remember that:
- Two lines are parallel if their slopes are the same.
- Two lines are perpendicular if their slopes are negative reciprocals.
- And two lines are neither (a.k.a intersecting) if they are neither parallel nor perpendicular.
We want to find the value of x such that
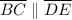 .
.
Therefore, the slopes of BC and DE must be equivalent.
So, let's find the slope of BC first.
BC)
We can use the slope formula:
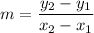
Let B(17, 5) be (x₁, y₁) and let C(11, -3) be (x₂, y₂). Substitute:
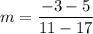
Subtract:
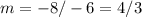
So, the slope of BC is 4/3.
DE)
Let D(-1, 2) be (x₁, y₁) and let E(x, -6) be (x, y₂). Substitute:
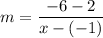
We know that the two slopes must be equal. So, the slope of DE must also be 4/3. Substitute 4/3 for m:
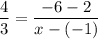
Solve for x. Simplify the right:

Cross multiply:
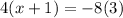
Multiply on the right:
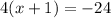
Divide both sides by 4:
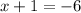
Subtract 1 from both sides:
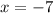
So, the value of x is -7.
And we're done!