The area, in square units, of triangle
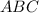 is
is
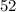 square units. Therefore, option C is correct
square units. Therefore, option C is correct
To find the area of triangle
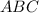 with vertices
with vertices
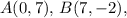 and
and
 , we can use the formula for the area of a triangle given by the coordinates of its vertices:
, we can use the formula for the area of a triangle given by the coordinates of its vertices:
![\[Area = (1)/(2) |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|\]](https://img.qammunity.org/2021/formulas/mathematics/high-school/4nrcbzy0sjeumpdglpya7pahw4fb6yc8aa.png)
where
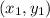 ,
,
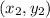 , and
, and
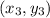 are the coordinates of the vertices
are the coordinates of the vertices
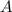 ,
,
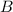 , and
, and
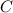 , respectively.
, respectively.
Let's calculate it.
To calculate the area of a triangle with vertices at given coordinates, we use the following formula derived from the determinant of a matrix:
![\[\text{Area} = (1)/(2) \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|\]](https://img.qammunity.org/2021/formulas/mathematics/high-school/bpubyw588b08o1jp3zzjhvnbe0823b39df.png)
The coordinates for the vertices
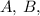 and
and
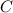 are
are
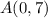 ,
,
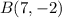 , and
, and
 respectively. Let's label them as follows:
respectively. Let's label them as follows:
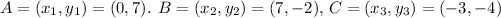
Now let's perform the calculation step by step:
1. Calculate the differences in y-coordinates between the vertices :

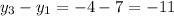
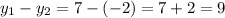
2. Multiply the x-coordinate of each vertex by the corresponding difference in y-coordinates calculated above:
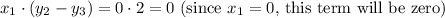
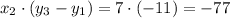
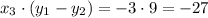
3. Sum up the results of the multiplications:
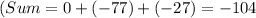
4. Take the absolute value and divide by 2 to get the area:
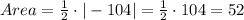
So, the step-by-step detailed calculation confirms that the area of triangle
 is
is
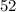 square units.
square units.