Answer:
P(Take the bus|Junior)=0.57
Explanation:
Conditional Probability
Is a measure of the probability of the occurrence of an event, given that another event has already occurred. If event B has occurred, then the probability that event A occurs is given by:
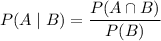
Where
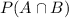 is the probability that both events occur and P(B) is the probability that B occurs.
is the probability that both events occur and P(B) is the probability that B occurs.
The two-way table shows statistics of students and we are interested to find the probability that, given the student is a junior (let's call it event B), they also take the bus (Event A). Thus, the probability we need to calculate is:
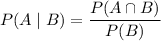
Checking on the table, we can see that both events occur when the row and the column of both events coincide, i.e. 20 students out of a total of 100 students in total. Thus:
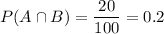
The probability that a student is classified as Junior is
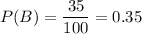
The conditional probability is:
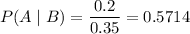
P(Take the bus|Junior)=0.57