Question

Find the foci of the hyperbola defined by the equation
`((x+8)^(2) )/(9) - ((y-7)^(2) )/(25) =1` . If necessary, round to the nearest tenth.

Answer 1

Foci: (-2.2, 7) and (-13.8, 7)

(nearest tenth)

Explanation:

General equation of a hyperbola

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

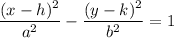
Center: (h, k)

Focal length equation: a² + b² = c²

Foci: (h ± c, k)

Given equation:

`((x+8)^2)/(9)-((y-7)^2)/(25)=1`

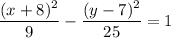
⇒ h = -8

⇒ k = 7

⇒ a² = 9

⇒ b² = 25

Focal length:

⇒ a² + b² = c²

⇒ 9 + 25 = c²

⇒ c = √34

Foci:

⇒ (h ± c, k) = (-8 ± √34, 7)

= (-2.2, 7) and (-13.8, 7)

**Refer to the attached graph**

Asymptotes are in red

Foci are in blue