Answer:
(a) Explained below.
(b) 0.0294
(c) 0.0173
(d) 0.09827
(e) 0.0452
Explanation:
The complete question is:
According to an airline, flights on a certain route are on time 80% of the time. Suppose 25 flights are randomly selected and the number of on-time flights is recorded.
(a) Explain why this is a binomial experiment.
(b) Find and interpret the probability that exactly 16 flights are on time.
(c) Find and interpret the probability that fewer than 16 flights are on time.
(d) Find and interpret the probability that at least 16 flights are on time.
(e) Find and interpret the probability that between 14 and 16 flights, inclusive, are on time.
Solution:
(a)
Let the random variable X be defined as the number of on-time flights.
A Binomial experiment has the following properties:
- There are a fixed number of trials (n).
- Each trial are independent of the others.
- Each trial has only two outcomes: Success and Failure
- Each trial has the same probability of success (p).
If a random variable X is used in an experiment and the experiment has all the above mentioned properties, then the random variable X is known as a binomial random variable.
All of these properties can be confirmed for the random variable X.
Thus, this is a binomial experiment.
(b)
Compute the probability that exactly 16 flights are on time as follows:
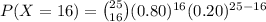
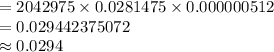
Thus, the probability that exactly 16 flights are on time is 0.0294.
(c)
Compute the probability that fewer than 16 flights are on time as follows:

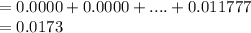
Thus, the probability that fewer than 16 flights are on time is 0.0173.
(d)
Compute the probability that at least 16 flights are on time as follows:
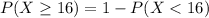
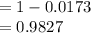
(e)
Compute the probability that between 14 and 16 flights, inclusive, are on time as follows:
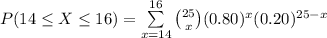
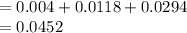
Thus, the probability that between 14 and 16 flights, inclusive, are on time is 0.0452.