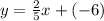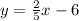Question

Which one would the equation be?

Answer 1

a.
`y = (2)/(5)x - 6`

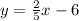
Explanation:

The slope-intercept form of equation of a line is given as
`y = mx + b`. Where,

m = slope

b = y-intercept.

Rewrite the equations,
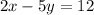`2x - 5y = 12` and
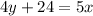`4y + 24 = 5x`, in the slope-intercept form by making y the subject of the formula. Then, derive our new equation that has the same slope as the first equation, and the same y-intercept as the second equation.

`2x - 5y = 12`

`2x - 12 = 5y`

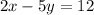
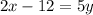
Divide both sides by 5

`(2x - 12)/(5) = (5y)/(5)`

`(2x)/(5) - (12)/(5) = y`

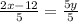
Rewrite

`y = (2x)/(5) - (12)/(5)`

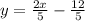
The slope of
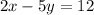`2x - 5y = 12` is ⅖.

`4y + 24 = 5x`

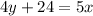
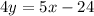`4y = 5x - 24` (subtraction property of equality)

Divide both sides by 4

`(4y)/(4) = (5x - 24)/(4)`

`y = (5x)/(4) - (24)/(4)`

`y = (5x)/(4) - 6`

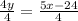
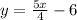
The y-intercet of
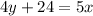`4y + 24 = 5x` is -6

Therefore, the equation that has the same slope as the first equation and the same y-intercept as the second equation would be:

`y = mx + b`

Plug in the values of m and b

`y = (2)/(5)x + (-6)`

`y = (2)/(5)x - 6`