Question

Parallelogram JKLM is reflected across a horizontal line through its center and then translated down and to the left to produce parallelogram QTSR

K
110°
R
S
9 ft
70°
M 12 ft
L
T
m
What is true about the angles and side lengths of parallelogram QTSR?
Enter the correct answers in the boxes

Answer 1

`\huge\boxed{Q = 110 \textdegree, \ ST = 9 \ \text{ft}}`

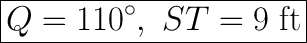
Explanation:

When we reflect and transform a figure, the angle lengths nor the side lengths are touched. The side length only changes if we dilate or stretch the figure, and the angle length only changes if we stretch the figure.

Therefore, we know the information is going to be the exact same. We just have to figure out what corresponds to what from JKLM to QTSR.

If we reflect a figure across a horizontal reflection line through its center, the figure will just flip sides. M will be J, L will be K, etc.

When we translate this down, nothing changes except its position. So we can pretend these two shapes are right on top of each other for now.

When we move these right on top of each other, we can see that Angle J overlaps with Angle Q. Since they don't have any weird intersects, we know that angle J will be equal to Angle Q. Since we already know J is 110°, we know Q is also 110°.

When we move it on top, we also see that KL overlaps with ST perfectly. Since we know KL is 9, that must mean ST is also 9.

Hope this helped!