Answer:
Prices of the two stocks A and B become same in 42 hours
Explanation:
Let t denotes number of hours in which the prices of the two stocks A and B become same.
Price of stock A = $15.59
Increase in price per hour = $0.12 t
Price of stock B = $16.34
Decrease in price per hour = $0.11 (t - 3)
(since price of stock A starts increasing per hour after 9 A.M. and price of stock B starts decreasing per hour after 12 noon that is 3 hours after 9 A.M.)
To find number of hours in which the prices of the two stocks A and B become same, solve
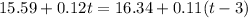
So, prices of the two stocks A and B become same in 42 hours